En esta lección vamos a aprender ¿Qué son los números reales? Cuáles son sus características y su clasificación, este contenido corresponde al bloque 1 del matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos
Contenido de la página
¿Qué son los números reales?
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales. Cualquier número real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real.
--- ---
Los números reales se representan mediante la letra R
Los números naturales y números enteros
Los primeros números que el ser humano utilizó para interpretar la realidad y cuantificarla fueron los naturales (N), 1, 2, 3, 4, 5… sucesivamente hasta el infinito, y que se usan de forma cotidiana.
Sin embargo, los números naturales positivos no se pueden aplicar a situaciones en las que tenemos que “quitar o restar”, pues para ello las cantidades se representan como negativas. +
--- ---
Al conjunto de números que incluyen los números negativos además de los positivos se le denomina números enteros (Z).
Los números racionales (Q)
Los números racionales son aquellos que se pueden expresar por el cociente o división de dos números enteros, es decir, mediante una fracción y pueden ser positivos, negativos o cero, por ejemplo:
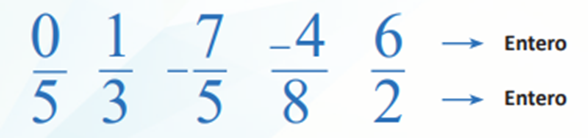
La expresión decimal de un número racional puede ser exacta o periódica. Por ejemplo, el número 2/3 expresado en forma decimal, es periódico. Si dividimos 2 ÷ 3 obtenemos 0.666…
--- ---
El número 6 se repite hasta el infinito ya que el residuo se repite una y otra vez; y para el número 20/11, si dividimos 20 ÷ 11 obtenemos 1.818181…, en donde los dígitos 8 y 1 se repiten indefinidamente.
En cambio, para 3/5, dividimos 3 ÷ 5 y obtenemos 0.6; para 8/5, la división que resulta da 1.6; en estas últimas divisiones se llega a un residuo igual a cero y la división se termina.
Todo número entero es un número racional (Q) pues lo podemos expresar como cociente, por ejemplo, el número 7 lo podemos escribir como 7 1 pues resulta de dividir 7 ÷ 1 = 7
--- ---
Los números irracionales (I)
Un número real irracional es aquel que no se puede escribir en fracción. Además en él los decimales se repiten sin presentar ninguna periodicidad. Un ejemplo de número irracional es π (Pi), cuyo valor es: 3.14159265358979 32384626433832795…, aunque en general se usa 3.1416 para hacer los cálculos correspondientes.

Como podemos notar, en los números irracionales los decimales siguen hasta el infinito sin mostrar ningún patrón, se representan indefinidamente con expresiones decimales infinitas no periódicas, a diferencia de los racionales, que pueden representarse con expresiones decimales periódicos.

3 comentarios