En esta lección vamos a aprender las operaciones con números reales que puedes realizar, este contenido corresponde al bloque 1 de Matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.
Contenido de la página
Operaciones con números reales
Veamos en seguida cuales son las operaciones que podemos realizar con los números reales.
--- ---
Suma
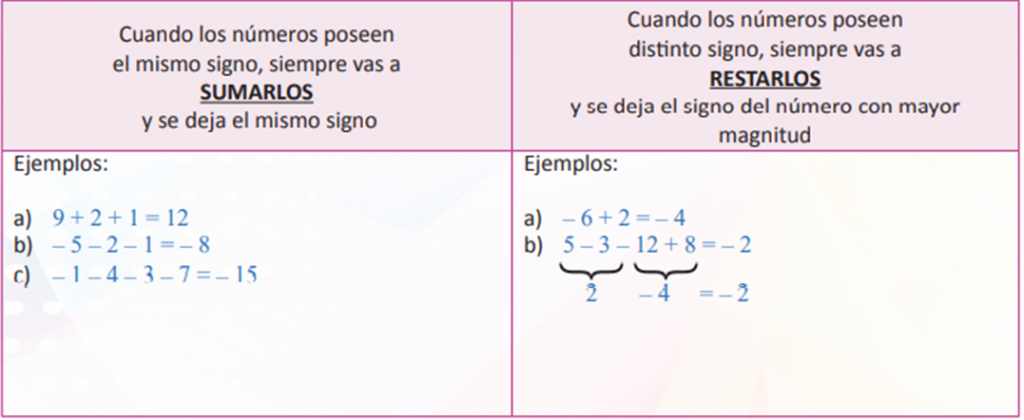
La suma o adición de dos números de igual signo se realiza sumando sus valores absolutos y poniendo al resultado el signo común. Por ejemplo: 3 + 7 = 10; –4 – 9 = –13.
El signo + puede omitirse en los números positivos cuando se encuentran al inicio, como con los casos del tres y el diez del primer ejemplo anterior. Cuando sumamos un número negativo debemos colocar siempre el signo menos, como en el menos cuatro y menos nueve del segundo ejemplo anterior (–4 – 9 = –13).
La suma o adición de dos números con signo diferente se realiza efectuando una resta de los valores absolutos de ambos números y al resultado se le antepone el signo del número que tenga mayor valor absoluto.
--- ---
8 + –15 = 8 – 15 = –7
–4 + 10 = 6
21 + –16 = 21 – 16 = 5
--- ---
Resta
La resta o sustracción puede expresarse en términos de la suma, puesto que, en general, podemos verla como una suma de números con signo diferente, como en el último de los ejemplos anteriores, que puede verse como la suma de dos enteros 21 y – 16; o como la resta de dos naturales, 21 y 16 = 5. Observa que esta última es la resta que ya conoces, 21 – 16 = 5.
Ahora bien, la operación de restar un número negativo será equivalente a la de sumar un número positivo (– – = +).
14 – –9 = 14 + 9 = 23
--- ---
6 – –5 = 6 + 5 = 11
Leyes de los signos en las sumas y restas
Multiplicación
La multiplicación o producto de dos números reales de igual signo siempre dará como resultado un número positivo. + × + = +, – × – = +.
6 × 8 = 48
--- ---
–7 × –3 = 21
La multiplicación o producto de dos números reales de distinto signo dará como resultado un número negativo. + × – = –, – × + = –
5 × –7 = –35
--- ---
–9 × 6 = –54
División
La división o cociente es la operación inversa de la multiplicación y consiste en averiguar cuántas veces un número (divisor) está contenido en otro número (dividendo). Si divides 20 (dividendo) entre 5 (divisor), el resultado es 4 (cociente), porque 20 ÷ 5 = 4; 4 × 5 = 20.
Como se resuelve una división
Para dividir números para los que la división no es exacta se utiliza el algoritmo de la división, que se explica a continuación mediante un ejemplo.
--- ---
Si queremos dividir 3465 entre 129, colocamos al dividendo, 3465, dentro de un semirectángulo (“la casita”), y al divisor afuera, como se muestra en la figura:

Se toman del dividendo solamente los números necesarios para que “quepa” el divisor. En este caso tomo 346, 129 cabe 2 veces. Pongo un 2 encima del 6 y multplico 2 por 129. El resultado lo coloco debajo de 346 para restárselo. Resto:
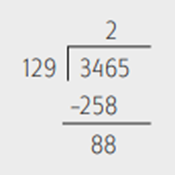
El 5 que queda en las unidades lo coloco al lado del 88 y obtengo 885. 129 cabe 6 veces en 885. Pongo un 6 encima del 5 del dividendo y multiplico 6 por 129. El resultado lo coloco debajo de 346 para restárselo.
--- ---
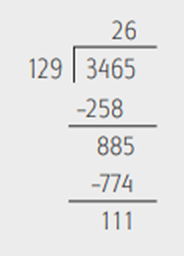
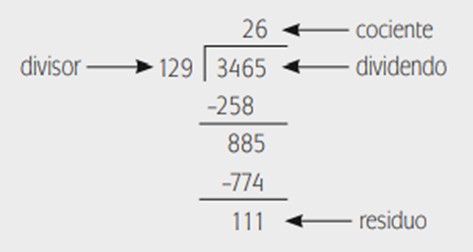
Terminamos! Al resultado se le llama cociente y a lo que sobró se le llama residuo
Resolver una división con decimales
Recuerda que si tenemos decimales en el divisor debemos quitar el punto decimal del mismo, para lo que debemos desplazar el punto del dividendo (si lo hay) tantos lugares a la derecha como cifras decimales tenga el divisor. Si no hay decimales en el divisor, o no los suficientes, se añaden ceros.
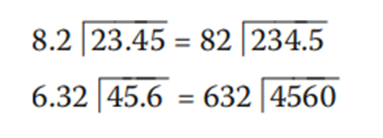
Después se procede a realizar la división subiendo el punto decimal al cociente, en el mismo lugar en el que se encuentra en el dividendo. La división entre cero no está definida. Por ejemplo, 6 ÷ 0 no tiene solución porque no existe ningún número real que multiplicado por 0 sea igual a 6. La división puede interpretarse en términos de la multiplicación a partir del inverso multiplicativo del divisor. Las reglas de los signos se aplican del mismo modo que en la multiplicación. Ejemplos
--- ---
–36 ÷ 4 = –9
40 ÷ –5 = –8
–28 ÷ –7 = 4
--- ---
Potenciación
La potencia es el resultado que se obtiene al multiplicar un número dos o más veces por sí mismo.
En particular, la potencia dos, o cuadrado, de un número se obtiene al multiplicarlo por sí mismo y se denota escribiendo un dos pequeño en la parte superior derecha de dicho número. Por ejemplo, el cuadrado de cinco se escribe de la siguiente forma: 52 = 5 × 5 = 25; y el cuadrado de menos tres se escribe –32 = –3 × –3 = 9.
La tercera potencia, o el cubo, de un número se obtienen al multiplicarlo por sí mismo y el resultado de nuevo por el número original, como en los siguientes ejemplos:
--- ---
73 = 7 × 7 × 7 = 49 × 7 = 343
43 = 4 × 4 × 4 = 16 × 4 = 64
La potencia cuarta se obtiene multiplicando un número por sí mismo, el resultado de nuevo por el mismo número y el nuevo resultado por el número original, y así sucesivamente para las potencias que siguen.
--- ---
34 = 3 × 3 × 3 × 3 = 9 × 3 × 3 = 27 × 3 = 81
–64 = –6 × –6 × –6 × –6 = 36 × –6 × –6 = –216 × 6 = 129
El número pequeño colocado en la parte superior, que identifica a la potencia, recibe el nombre de exponente; el número que multiplicamos por sí mismo se llama base. El exponente indica cuántas veces debe multiplicarse la base por sí misma.
--- ---
Cuando se eleva un número negativo a una potencia par el resultado será positivo, sin embargo, si se eleva un número negativo a una potencia impar el resultado será negativo. Las potencias pares siempre son positivas debido a las propiedades de la multiplicación, que, como ya lo estudiaste, dicen que el producto de dos negativos da como resultado un número positivo – × – = +, es decir, que por cada dos signos – obtengo +: –25 = –2 × –2 × –2 × –2 × –2 = 4 × 4 × –2 = –32, en cambio, las potencias impares siempre dan un resulta[1]do negativo.
Leyes de los signos en las multiplicaciones y divisiones

Radiación
La operación inversa de la potencia, que es la raíz. Esto significa que si:
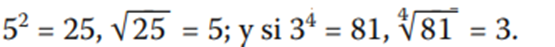
Las raíces cuadradas de números enteros tienen dos posibles resultados, el valor positivo y el negativo. Por ejemplo, existen dos números enteros que satisfacen que su cuadrado sea igual a 16, el 4 y el –4, porque 42 = 4 × 4 = 16 y también –42 = –4 × –4 = 16.
--- ---
Propiedades de la radiación
1. Para n par, no está definida si x < 0, es decir, si x es negativo.
No existe ningún número que al multiplicarse por sí mismo un par de veces dé como resultado un número negativo, debido a que al multiplicar un número por sí mismo, sea este negativo o positivo, el resultado siempre es positivo.
Ejemplo: √–36 no está definida para los números reales, porque no existe un número que al multiplicarse por sí mismo tenga como resultado –36. Piensa en 6 o en –6, por ejemplo, al elevarlos al cuadrado obtienes 36. Lo mismo ocurre para la cuarta potencia.
--- ---
Ejemplo: 4 √–81 no está definida para los números reales, porque no existe un número que al multiplicarse por sí mismo cuatro veces dé –81. El 3 o el –3, por ejemplo, al elevarlos a la cuarta potencia, obtengo 81.
3 × 3 × 3 × 3 = 81; –3 × –3 × –3 × –3 = 81 (por ser potencia par).
2. Las raíces del cero son iguales a cero para cualquier n: n √ 0 = 0
--- ---
3. Las raíces impares de números positivos son positivas: n √ x > 0 si x > 0 y n es impar. Ejemplo: 3 √ 27 = 3
4. Las raíces impares de números negativos son negativas: n √ x < 0 si x < 0 y n es impar. Ejemplo: 3 √–27 = –3
Conceptos básicos de exponentes y radicales
Así como las leyes de los signos, las leyes de los exponentes te serán de gran ayuda para resolver con éxito muchas operaciones. A continuación, se presentan consideraciones básicas sobre dos temas relacionados entre sí: exponentes y radicales
--- ---
Cuando se eleva un número a un exponente se le llama potencia y significa multiplicar ese número la cantidad de factores que se indica. Ejemplos:

La raíz “n” de un número es igual a otro número que elevado a “n” resulta el primero. Ejemplos:

Jerarquización de operaciones con números reales
Cuando realizamos operaciones con los números reales debemos tener en cuenta que solo podemos realizar una operación a la vez, de modo que es necesario saber cuál es el orden correcto de las operaciones que aparezcan en una misma expresión.
--- ---
Este orden se denomina jerarquía de las operaciones o regla de prioridad. Esta regla o jerarquía establece un orden de importancia para ejecutar las operaciones como se muestra a continuación
Primero: Resolver todos los signos de agrupación: Paréntesis () Corchetes [ ] Llaves { }
Segundo: Resolver todas las potencias y raíces
--- ---
Tercero: Resolver todas las multiplicaciones y divisiones
Cuarto: Resolver todas las adiciones (sumas) y sustracciones (restas)
Un ejemplo clásico lo encontramos constantemente en internet y las redes sociales:
--- ---
¿Cuál es el resultado de la siguiente operación?
4 + 6 ÷ 2 – 1 × 5 = ?
Un error común es querer resolver las operaciones como van apareciendo de izquierda a derecha, obteniendo resultados equivocados como 20, 50 o 30, cuando lo correcto es aplicar la jerarquización, en este caso, primero multiplicando y dividiendo, dejando para lo último las sumas y restas.
--- ---
4 + 6 ÷ 2 – 1 × 5 = 4 + 3 – 5 = 2

6 comentarios