En esta lección vamos a aprender las operaciones con fracciones que puedes realizar, este contenido corresponde al bloque 1 de Matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.
Los números racionales en forma de fracciones comparten las propiedades de los números enteros, sin embargo, para realizar operaciones con ellos se requiere conocer algunas de sus particularidades.
Contenido de la página
--- ---
¿Qué son las fracciones?
Las fracciones se componen de numerador y denominador. El denominador representa la cantidad de partes en que se ha dividido la unidad, y el numerador es la cantidad que se toma de éstas.
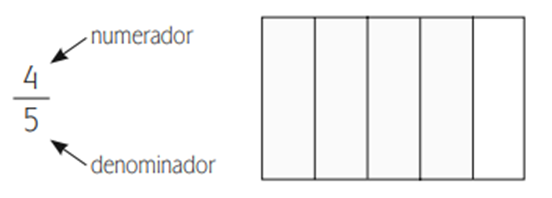
El rectángulo del dibujo anterior se ha dividido en 5 partes iguales (denominador) y se han tomado 4 de éstas (numerador)
Fracciones equivalentes
Las fracciones equivalentes son aquellas que tienen el mismo valor, aunque parezcan diferentes. Ejemplo: ¾ = 6/8
--- ---
Puedes probar que las fracciones anteriores son iguales efectuando las divisiones correspondientes: 3 ÷ 4 = 0.75; del mismo modo: 6 ÷ 8 = 0.75. También puedes pensarlo como que tres cuartas partes de una pizza es la misma cantidad que seis octavas partes de una pizza del mismo tamaño.
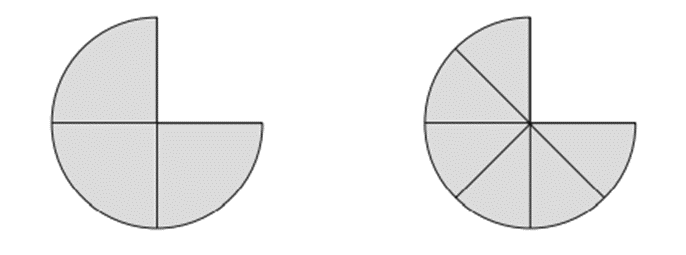
Observa que en la segunda fracción tanto el numerador como el denominador están multiplicados por 2, con respecto de aquellos de la primera fracción. También serían fracciones equivalentes las siguientes: 3/4 = 9/12 . Esta vez el numerador y el denominador están multiplicados por 3.
Serán fracciones equivalentes a 3/4 todas aquellas fracciones que resulten de multiplicar al numerador y al denominador por el mismo número entero.
--- ---
En general, dos fracciones son equivalentes si cumplen lo siguiente:
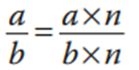
Siendo n un número entero.
Operaciones con fracciones
Suma y resta de fracciones
La suma (o la resta) de fracciones con un denominador común, es un número racional cuyo numerador es la suma (o resta) de los numeradores y cuyo denominador es el denominador común.
--- ---
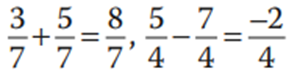
Y para dos números racionales cuyo denominador no es común, la suma (o resta) se define de la siguiente manera:
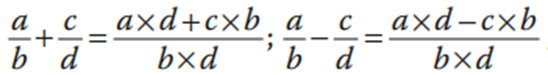
Suma y resta con mínimo común múltiplo Un método alternativo para resolver sumas y restas de fracciones, es utilizando el mínimo común múltiplo (m. c. m.) de los denominadores, en lugar de multiplicarlos. El mínimo común múltiplo de dos o más números es el menor múltiplo común distinto de cero. Para encontrarlo se debe descomponer el número en factores primos tal como estudiantes en las primeras lecciones. Ejemplos: El m.c.m. de 5, 6 y 4 se obtiene:
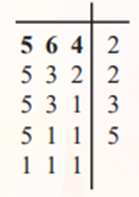
m.c.m. = 2x2x3x5 = 60
--- ---
En consecuencia, 60 representa el número más pequeño que puede dividirse exactamente entre 5, 6 y 4
Sumar las siguientes fracciones: 3/5 + 1/6 – ¾ como ya se tiene el m.c.m, entonces:
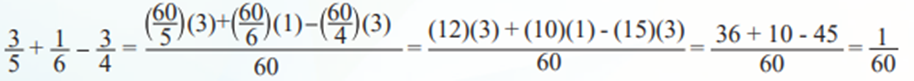
Multiplicación de fracciones
La multiplicación o producto de dos fracciones es otro número racional que tiene por numerador el producto de los numeradores y por denominador el producto de los denominadores
--- ---
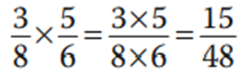
División de fracciones
La división de dos números racionales es otro número racional que tiene por numerador el producto del numerador del primero con el denominador del segundo, y por denominador el producto del denominador del primero con el numerador del segundo
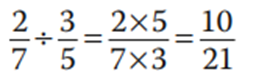
Las flechas en la siguiente imagen te pueden ayudar a que no olvides cómo se efectúan la multiplicación y la división.

