Qué es la recta numérica y para qué sirve – ejemplos de la recta numérica

En esta lección vamos a aprender ¿Qué es la recta numérica y para qué sirve? Conoceremos algunos ejemplos, este contenido corresponde a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.

Qué es la recta numérica y para qué sirve

La recta numérica es aquella que se usa para representar geométricamente los números y las operaciones que se pueden hacer con ellos.

En ella los números enteros son como puntos que están separados de manera uniforme y ordenada. Se elige un punto arbitrario, denominado origen, que representa al 0 y un punto a la derecha que representa al 1.

Los demás enteros se colocan tomando como unidad la distancia entre 0 y 1. Para trabajar en la recta, los números enteros se ordenan de menor a mayor valor a partir del origen.

Así, los números que están a la izquierda de un entero son menores a él y los que están a la derecha mayores a él; explicado de otra forma se diría que dados dos números enteros a y b, únicamente puede ocurrir una de las siguientes tres posibilidades, a = b (a es igual a b), a< b (a es menor que b) o a > b (a es mayor que b).

La recta también es útil cuando se intenta entender cómo se transforman los números al realizar operaciones.

Además de los números enteros es posible representar otros conjuntos de números. En la representación de los números racionales se establece que a cada punto de la recta le corresponde un número racional único.

De manera recíproca a cada número racional le corresponde un único punto de la recta, dependiendo de la magnitud del número y la distancia que concierne a esta magnitud a partir del cero.

Entre cada dos números enteros es posible colocar un infinito de números, tanto racionales como irracionales. Por ejemplo, entre el 0 y el 1 podríamos colocar los números 3/4, 1/2, 1/4 entre otros.

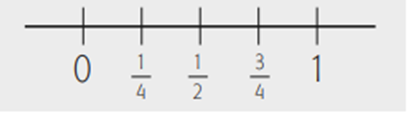
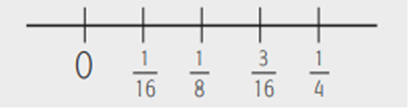
Así, entre cualesquiera dos números racionales, existe una cantidad infinita de números, por ejemplo, entre 1/4 y 1/2 iría 1/3; y entre 3 4 y 1 iría 4/5, y así sucesivamente; podríamos colocar una cantidad infinita de números racionales y no solamente entre cada dos enteros sino además entre cada dos números racionales. Si ahora dibujamos con mayor amplitud el intervalo entre 0 y 1/4, entonces se puede colocar un infinito de números racionales intermedios, tal y como se muestra a continuación:

El valor absoluto

Para hacer operaciones con los números, en ocasiones solamente se requiere conocer su valor, sin importar si es positivo o negativo. Para hacerlo piensa en una persona que entra a un edificio por la planta baja y luego baja 3 pisos, al mismo tiempo entra otra persona a la planta baja y sube 3 pisos.

En ambos casos, las personas caminaron 3 pisos. Si el interés recae en saber la distancia recorrida, sin importar en qué sentido lo hicieron, entonces el valor es el mismo (3) y se le denomina valor absoluto.

Entonces, éste representa la distancia que hay del origen, o cero, o dicho número de la planta baja al 3 y al -3. La distancia del origen al tercer piso es 3; asimismo, la distancia del origen al sótano 3 también es 3; aunque tienen un sentido diverso, como se muestra en la figura.

El valor absoluto de cualquier número real diferente de cero siempre es positivo y cuando se considera el valor absoluto se representa mediante dos barras verticales que encierran al número, como se muestra en los siguientes ejemplos. Valor absoluto es simplemente la distancia que hay de un número al cero: |5| = 5, |–5| = 5. Tanto el 5 positivo como el 5 negativo están a “5” del cero. |–8| = 8, |8| = 8, |0| = 0, |–6.2| = 6.2, |6.2| = 6.2