En esta lección vamos a conocer Como obtener el Mínimo común múltiplo (MCM) y el Máximo común divisor (MCD), este contenido corresponde al bloque 1 de Matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.
Contenido de la página
¿Qué es el mínimo común múltiplo y ejemplos?
Mínimo Comun Multiplo definicion: El mínimo común múltiplo (MCM) de dos o más números es el menor múltiplo común distinto de cero, es decir, es el número más pequeño que resulta de la multiplicación de cualquiera de los dos números.
--- ---
¿Cómo obtener el Mínimo común múltiplo (MCM)?
Ejemplo: El MCM de 24 y 36:
Los múltiplos de 24 son: 24 (resultado de 24 × 1), 48 (de 24 × 2), 72 (de 24 × 3), 96 (de 24 × 4), etcétera. Los múltiplos de 36 son: 36 (producto de 36 × 1), 72 (de 36 × 2), 108 (36 × 3), etcétera.
El número más pequeño, común a ambas listas de múltiplos es 72; por lo tanto: MCM (24, 36) = 72
--- ---
Para encontrar el MCM de dos o más números, debemos obtener la descomposición en factores primos de éstos y tomar a todos los números que aparezcan en al menos una de las descomposiciones, elevado a la potencia que sea la máxima.
Por ejemplo, si queremos encontrar el MCM de 24 y 36
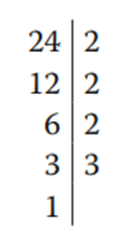
24 = 2 × 2 × 2 × 3 = 23 × 3
--- ---
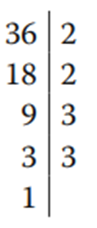
36 = 2 × 2 × 3 × 3 = 22 × 32
Aquí aparecen los números 2 y 3 en ambas descomposiciones. Para el 2 la potencia máxima es 3 y para el 3 es 2. Por lo tanto el MCM se obtiene multiplicando 23 × 32 = 72
¿Qué es el Máximo común divisor (MCD)?
El máximo común divisor (MCD) de dos o más números es el número más grande posible que es divisor de todos ellos.
--- ---
Como sacar el máximo común divisor de dos números
Ejemplo:
El MCD de 24 y 36:
Los divisores de 24 son: 1, 2, 3, 4, 6, 8, 12 y 24
--- ---
Los divisores de 36 son: 1, 2, 3, 4, 6, 9, 12, 18 y 36
El número más grande que divide a ambos es 12, por lo tanto: MCD (24, 36) = 12
Al igual que en el caso del MCM, la descomposición en factores primos resulta muy útil para encontrar el MCD de dos o más números. En este caso, debemos obtener la descomposición en factores primos de éstos y tomar a todos los números que aparezcan en todas las descomposiciones, elevados a la potencia que sea la mínima.
--- ---
Por ejemplo, si queremos encontrar el MCD de 24 y 36:
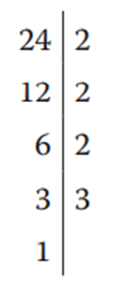
24 = 2 × 2 × 2 × 3 = 23 × 3
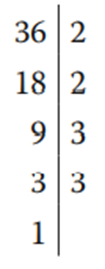
36 = 2 × 2 × 3 × 3 = 22 × 32
--- ---
Tenemos 2 y 3 en ambas descomposiciones. Para 2 la potencia mínima es 2 y para 3 es 1.
Por lo tanto, el MCD es: 22 × 3 = 12
Tip para obtener el Mínimo común múltiplo (MCM) y el Máximo común divisor (MCD)
Para encontrar tanto el MCM como el MCD, se usa un procedimiento similar: descomponer los dos números en primos y utilizar todos los números que aparecen elevados a una potencia:
--- ---
En el mínimo común múltiplo utilizas los números primos con la potencia mayor. De este modo, solo incluimos los números que aparecen en todas las descomposiciones.
En el máximo común divisor empleas los números primos con la menor potencia. De este modo, incluimos los números que aparecen aunque sea en una de las descomposiciones.
Si te confunde cuándo usar la mayor o la menor potencia, piensa que la lógica es cruzada: ¡para el mínimo utilizas la máxima, y para la máxima, el mínimo!
--- ---

1 comentario