En esta lección vamos a conocer los números primos y los números compuestos, este contenido corresponde al bloque 1 de Matemáticas del primer semestre y a la unidad 1 de la materia de Representaciones simbólicas y algoritmos.
Contenido de la página
¿Qué son los números primos?
Los números primos son aquellos que solo son divisibles por sí mismos y por el 1. Ejemplos de números primos: 5, 13, 23.
--- ---
Como encontrar números primos usando la Criba de Eratóstenes.
Para este ejemplo vamos a encontrar todos los números primos entre el 1 y el 50.
Primero escribe una tabla con todos los números del 1 al 50:

El 1 no es considerado ni primo ni compuesto, por lo tanto lo eliminamos de la lista. El 2 es número primo, sin embargo, sus múltiplos no lo son pues lo tienen a él como divisor. Entonces elimina del listado todos los números que son pares, es decir, múltiplos de dos.
--- ---

El siguiente número primo es el 3, pero sus múltiplos no lo son. Elimina entonces de la tabla los múltiplos de 3 que no se hayan tachado antes, es decir, los múltiplos de 3 que no son pares, como el 9 el 15, etcétera.

El siguiente número primo es el 5, y también tachamos a sus múltiplos, de los cuales solo quedaban sin tachar el 25 y el 35
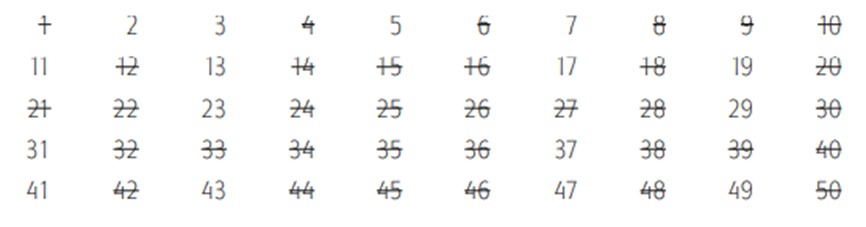
El siguiente número primo es el 7 y solamente queda un múltiplo suyo por quitar de la lista, el 49, ¡táchalo!
--- ---
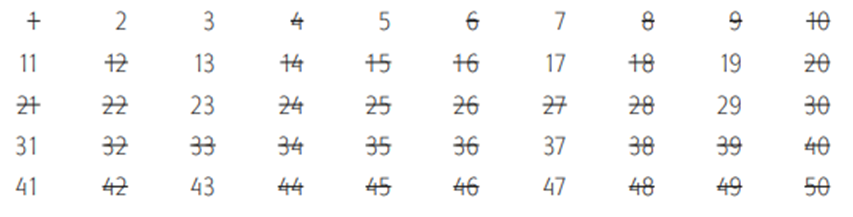
El número primo que sigue es el 11 y sus múltiplos previos a 50 ya han sido eliminados. Por lo tanto, los números que quedan son todos primos, es decir que según la Criba de Eratóstenes los números primos entre 1 y 50 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
¿Qué son los números compuestos?
Los números compuestos se llaman así porque se componen del producto de números primos. Es como si los números primos fueran la materia prima para construir al resto de los números mediante multiplicaciones.
Por ejemplo, el 6 se obtiene de multiplicar al 2 y al 3. El 12 se obtiene al multiplicar el 6 por 2. Por lo tanto, el 12 = 2 × 2 × 3. Así, cada número compuesto puede descomponerse en una multiplicación de números primos que es única para dicho número. Se pueden utilizar exponentes para escribir esta descomposición en una manera simplificada.
--- ---
Ejemplos:
36 = 2 × 2 × 3 × 3 = 22 × 32
50 = 2 × 5 × 5 = 2 × 52
--- ---
30 = 2 × 3 × 5
49 = 7 × 7 = 72
Descomposición en factores primos
Una herramienta que nos será muy útil a lo largo del tema de divisibilidad es la descomposición en factores primos. Ésta tiene aplicaciones prácticas en muchos campos. Se utiliza para encontrar divisores y múltiplos, para encontrar el común denominador en operaciones con fracciones, para la simplificación de fracciones, y en los últimos años su mayor aplicación está en la criptografía.
--- ---
La descomposición en factores primos es el producto de números primos que dan como resultado un cierto número natural. Cada número natural tiene una única descomposición en factores primos
¿Cómo puedo encontrar la descomposición en factores primos de un número determinado?
Se trata de partir al número en los números primos que lo dividen. Si quiero encontrar la descomposición en factores primos de un número tengo que encontrar los números primos que lo dividen. Empiezo dividiendo por 2 todas las veces que se pueda, sigo con 3, luego con 5 y así sucesivamente, utilizando números primos del menor al mayor hasta que no pueda dividir más.
Por ejemplo, la descomposición en factores primos del 24 se efectúa así:
--- ---
Escribo el número y trazo una línea a su derecha; 24 es divisible por 2, por lo tanto coloco un 2 del lado derecho de la línea y divido entre 2. El resultado, 12, lo escribo debajo del 24. 12 también es divisible por 2, por lo tanto coloco un 2 al lado derecho del 12 y divido entre 2. El resultado, 6, lo coloco debajo del 12. Vuelvo a dividir entre 2, puesto que 6 también es divisible entre 2, y escribo el resultado, 3, que al ser primo solamente se puede dividir entre 3. Escribo un 3 a su lado derecho y divido entre 3 quedando como resultado 1.
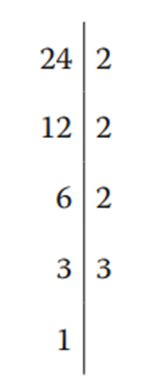
El resultado de la descomposición es la multiplicación de los números primos que se obtuvieron. Para escribirla de forma sintética, se utilizan exponentes. Por lo tanto: 24 = 2 × 2 × 2 × 3 = 23 × 3.
La descomposición en factores primos de 60 es la siguiente:
--- ---
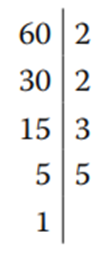
Por lo tanto: 60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
