Qué es el lenguaje algebraico

En esta lección vamos a conocer qué es el lenguaje algebraico, este contenido corresponde al bloque 4 de Matemáticas del primer semestre y a la unidad 2 de la materia de Representaciones simbólicas y algoritmos.

Veamos un ejemplo: Joaquín quiere analizar las ventas de camisetas de una tienda, cuando recibe el inventario observa que el informe indica 2 camisetas vendidas en la primera hora, al pasar la segunda hora se han vendido 5, después 8 y en la cuarta hora 11.

Si observas el ejemplo te darás cuenta que para el primer término que es a₁ existe un valor específico que indica la cantidad de camisetas vendidas en la primera hora (2 camisetas). Mientras que cuando se habla de las camisetas vendidas en cualquier hora entonces se le asigna la letra n y aparece un número que se representa con una letra.

Qué es el lenguaje algebraico – conceptos que debes dominar

A un número que se representa con una letra se le llama literal.

Ahora es importante que analices los siguientes conceptos:

Literal

Es una letra asignada a un valor numérico que puede ser conocido o no.

Ejemplo 1: La diferencia entre las camisetas vendidas entre cada hora es de 3. d = 3

Ejemplo 2: En un granero hay vacas y ovejas. G = granero

V = Vacas O = Ovejas G = V + O

Variable

Es una letra asignada a una magnitud que puede variar si cambiamos los elementos que influyen en dicha magnitud.

Ejemplo: El perímetro de un círculo se calcula multiplicando el diámetro por π.

P = Perímetro del círculo D = Diámetro

P = D • π Si varias el valor del diámetro entonces variará el valor del perímetro, de ahí que obtiene su nombre, variable.

Incógnita

Es una letra asignada a un valor numérico específico para una situación determinada, que en principio es desconocido y puede calcularse.

Ejemplo: ¿Cuál es el 80% de 400?

X = 80% de 400

X = (0.80)(400)

X = 320

¿Cuál es el objetivo del lenguaje algebraico?

El lenguaje algebraico tiene como objetivo extraer la información de una situación de tal manera que se pueda representar como una expresión matemática que se opere y analice utilizando las propiedades de los números. Analiza la siguiente tabla para que identifiques y observes las palabras clave para representar distintas operaciones:

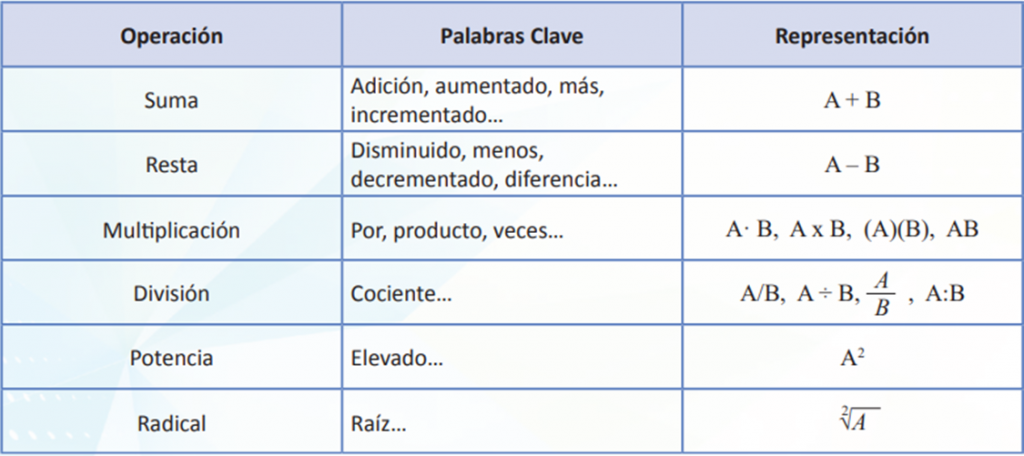
¿Qué son las Expresiones algebraicas?

A las expresiones que involucran operaciones con números desconocidos se les denomina expresiones algebraicas. Cuando éstas llevan el signo que denota igualdad se les conoce como ecuaciones y son éstas las que permiten solucionar problemas.

Para resolver ecuaciones es básico saber manipular de manera adecuada cualquier tipo de expresiones algebraicas. En ese sentido, habría que tener claro qué se puede hacer y qué no se puede hacer al trabajar expresiones algebraicas complejas.

Una expresión algebraica es, pues, un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas, tal y como se muestra en los siguientes ejemplos:

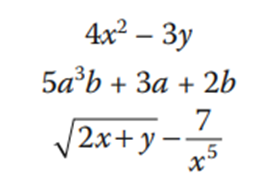
Una expresión algebraica se forma a partir de términos algebraicos separados entre sí por los signos de + y –.

A un término algebraico lo conforman un coeficiente numérico y una parte literal. El coeficiente numérico es la cantidad numérica que se encuentra a la izquierda de la parte literal, y que indica la cantidad de veces que ésta se debe sumar o restar dependiendo del signo que tenga.

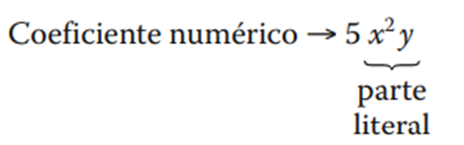
Así, por ejemplo, si se analiza la expresión 7x⁴ se tiene que:

En el primer término, el coeficiente numérico es 7 y ello quiere decir que x4 se suma siete veces: 7x⁴ = x⁴ + x⁴ + x⁴ + x⁴ + x⁴ + x⁴ + x⁴

La parte literal de una expresión algebraica está constituida por las letras y sus exponentes.

Por ejemplo, para el término 7x⁴ la parte literal corresponde a x⁴ = x × x × x × x, y para el término –3n² la parte literal es n² = n × n

El grado de un término algebraico es la suma de los exponentes de los factores de la parte literal. Por ejemplo: 5x es un término de primer grado, o de grado 1 Recuerda cuando el exponente o el coeficiente numérico es 1, no lo escribimos. Por lo tanto, x significa que se suma una vez (porque su coeficiente numérico es 1) y que se multiplica por sí mismo una vez (porque su exponente es 1). La suma de los exponentes del término es 1.

En la expresión –9a³ b⁴ el grado del término es séptimo o siete. El exponente de a es 3 y el de b es 4. La suma de los exponentes es 3 + 4 = 7. 3mn es un término de segundo grado o de grado 2. El exponente de m es 1 y el de n, también es 1, por lo tanto, 1 + 1 = 2.

ab³ es un término de cuarto grado o de grado 4. El exponente de a es 1 y el de b es 3: 3 + 1 = 4.

8 es un término de grado 0, con cero literales. Recuerda que x0 es igual a 1.